Algebra- Bereken het percentage % Berekening van percentages
Hoeveel is X % van het getal Y?
Hoe bereken je het percentage van een getal?
De eenvoudige regel van drie kan ook worden gebruikt - Breuken in decimalen: hoe doe ik dat?
Elke gewone breuk met een noemermacht van 10 kan als een decimale breuk worden geschreven.
Hoe kan ik een breuk omzetten naar een decimaal getal?
Leer hoe u gewone breuken in decimale vorm schrijft.
Hoe converteer ik van decimaal naar binair? - De regel van drie
De eenvoudige regel van drie is de methode om de evenredigheid te bepalen.
De eenvoudige regel van derden is een wiskundige methode waarmee een van de voorwaarden van een evenredigheidsvergelijking kan worden bepaald op basis van de andere.
De regel keert terug om de vierde evenredigheid uit de verhoudingen te berekenen:
a/b=c/x - Rekenkundig gemiddelde
Formule
ma = (x1+x2+ ... + xn) / n
Als a,b en c reële getallen zijn, is hun rekenkundig gemiddelde ma = (a+b+c) / 3
Geometrie in de ruimte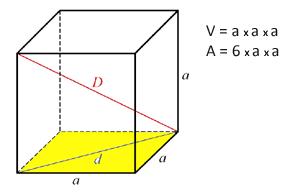 Gebied van de kubus
Hoe bereken je de oppervlakte van de kubus?
De oppervlakte wordt berekend: de oppervlakte van een vierkant (zijde tot vierkant - a2) en vermenigvuldig dit met 6.
A = 6*a2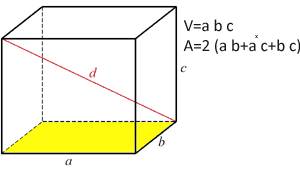 Gebied van het rechthoekige parallellepipedum
De totale oppervlakte van het rechthoekige parallellepipedum is 2*(oppervlakte van zijde ab + oppervlakte van zijde ac + oppervlakte van zijde bc)
Oppervlakte van zijde ab = a x b
Oppervlakte van zijde ac = a x c
Zijoppervlak bc = b x c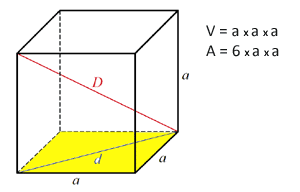 Het volume van de kubus
Hoe bereken je het volume van de kubus?
Wat is de formule en figuur.
Het volume is gelijk aan de oppervlakte van de basis vermenigvuldigd met de hoogte (vierkante zijde vermenigvuldigd met a - a2*a)
V = a*a*a = a3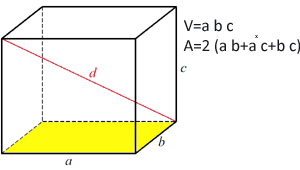 Het volume van het rechthoekige parallellepipedum
Het volume van het rechthoekige parallellepipedum wordt berekend door het oppervlak van de basis te vermenigvuldigen met de hoogte van het parallellepipedum
Volumeformule:
V=a*b*c
Trigonometrie Cosinus - cos(x) - cosinusfunctie
De cosinusfunctie wordt gedefinieerd in een rechthoekige driehoek als de verhouding tussen het aangrenzende been en de schuine zijde. De grafiek van de functie is een cosinus. De functie wordt gedefinieerd in het interval van -∞ tot ∞ en heeft waarden tussen -1 en 1. Sinus sin(x) - sinusfunctie
Berekent het resultaat Sine sin(x) - de sinusfunctie
Vlakke geometrie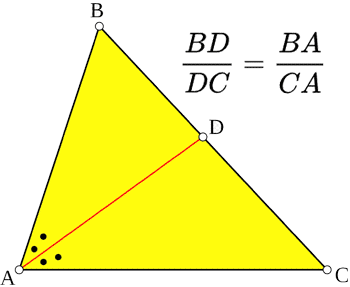 Bissectrice stelling
In een driehoek ABC bepaalt de bissectrice A aan de overstaande zijde (BC) segmenten die evenredig zijn met de zijden van de hoek BD/DC=BA/CA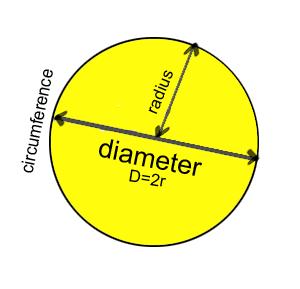 De diameter en omtrek van de cirkel
Formule
Doorsnede d = 2 × r
Omtrek C = π × d = 2 × π × r
Oppervlakte van de ronde schijf A = π × d²/4 = π × r²
Ï€ = 3,14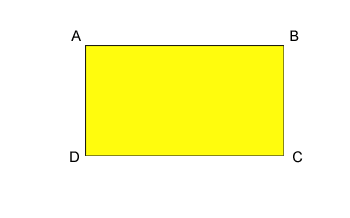 De omtrek van de rechthoek
De omtrek van de rechthoek wordt gedefinieerd als de som van de 4 zijden van de rechthoek
P=AB+BC+CD+DA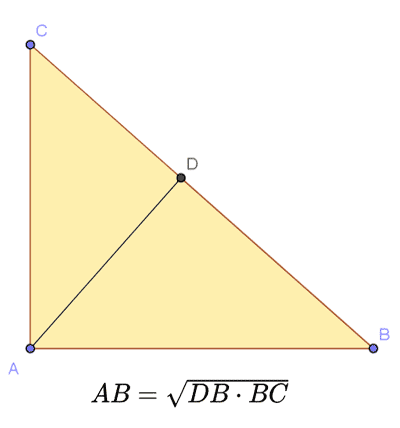 De stelling van de been
In een rechthoekige driehoek is de lengte van een been het geometrische gemiddelde tussen de lengte van zijn projectie op de hypotenusa en de lengte van de hypotenusa.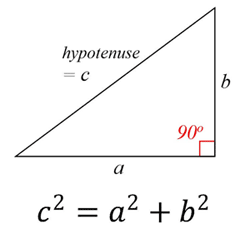 De stelling van Pythagoras
De stelling van Pythagoras stelt dat in elke rechthoekige driehoek de som van de kwadraten van de benen gelijk is aan het kwadraat van de schuine zijde (de zijde tegenover de rechte hoek).
Pythagoras-relatie:
a2 + b2 = c2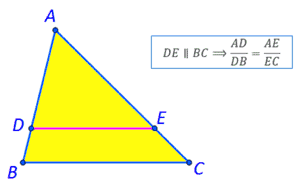 De stelling van Thales
Een parallel aan een van de zijden van een driehoek bepaalt aan de andere twee zijden, of aan hun verlengingen, proportionele segmenten.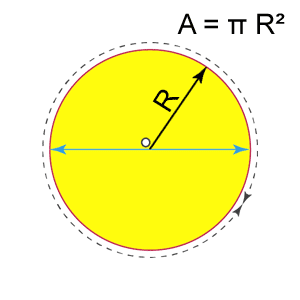 Gebied van de cirkel
Als de cirkel straal R heeft, is de oppervlakte π R²
A=πR²
De oppervlakte van een cirkel is gelijk aan pi (Ï€) vermenigvuldigd met de straal in het kwadraat.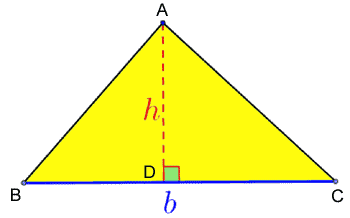 Gebied van de driehoek
Per definitie is de oppervlakte van een driehoek b * h gedeeld door 2, waarbij b de lengte van een zijde voorstelt en h de lengte van de hoogte die overeenkomt met die zijde. Gebied van de ellips
Per definitie is de oppervlakte van de ellips gelijk aan π × a × b, waarbij a, b de halve assen zijn, en π (pi) een wiskundige constante gelijk aan 3,14159 is.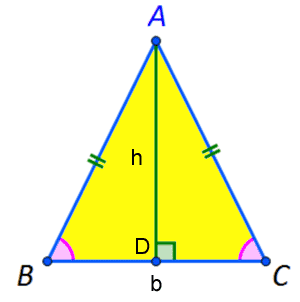 Gebied van de gelijkbenige driehoek
Oppervlakte = (b*h)/2
De oppervlakte is gelijk aan de basis (b) vermenigvuldigd met de hoogte (h) gedeeld door 2
De hoogte wordt gevonden door de stelling van Pythagoras uit de rechthoekige driehoek die wordt gevormd wanneer de hoogte loodrecht op de basis valt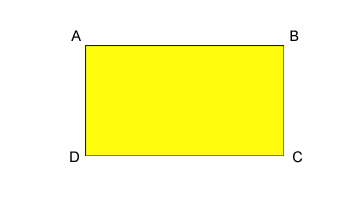 Gebied van de rechthoek
De oppervlakte wordt berekend door de lange zijde te vermenigvuldigen met de korte zijde
A = AB x BC
|
